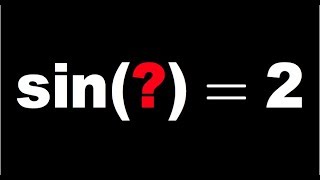We know the range of sin(x) is between -1 and 1, inclusively, but that's just with real numbers x. What if our input for the sine function is a complex number? In fact, we can derive the complex definition of sine from the Euler's formula and we can write sin(z) in terms of complex exponential (e^(iz)-e^(-iz))/(2i) and we will be able to solve sin(z)=2.

💪 Support this channel, https://www.patreon.com/blackpenredpen

This is my equation of the year in 2017.
To see others, please check out here 👉 https://www.youtube.com/playlist?list=PLj7p5OoL6vGxHsQjgCw5Nfe8O3o8fu3LV
#equationoftheyear

-ln(2+-sqrt(3)), https://www.youtube.com/watch?v=Me9yxROZbRQ
Euler's formula: https://www.youtube.com/watch?v=jF1Qv8KyZ1Q

Get an Euler's Identity t-shirt: https://amzn.to/427Seae

*Sorry I forgot the square root. |z| =sqrt(a^2+b^2)
**Also, I should have written the horizontal axis as "Re" and the vertical axis as "Im"
***The last time I did complex analysis was back in 2012