This is an audio version of the Wikipedia Article:
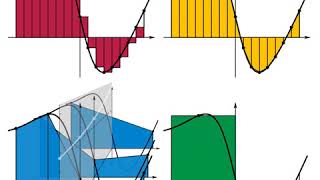
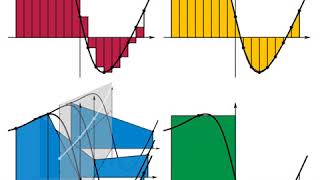
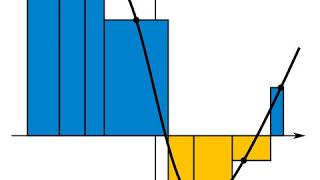
https://en.wikipedia.org/wiki/Integral


00:00:27 1 History
00:00:55 1.1 Pre-calculus integration
00:01:09 1.2 Newton and Leibniz
00:01:37 1.3 Formalization
00:02:05 1.4 Historical notation
00:02:19 2 Applications
00:02:47 3 Terminology and notation
00:03:01 3.1 Standard
00:03:29 3.2 Meaning of the symbol idx/i
00:03:57 3.3 Variants
00:04:53 4 Interpretations of the integral
00:05:07 5 Formal definitions
00:05:35 5.1 Riemann integral
00:06:17 5.2 Lebesgue integral
00:06:45 5.3 Other integrals
00:07:13 6 Properties
00:07:27 6.1 Linearity
00:07:55 6.2 Inequalities
00:08:09 6.3 Conventions
00:08:23 7 Fundamental theorem of calculus
00:09:05 7.1 Statements of theorems
00:09:33 7.1.1 Fundamental theorem of calculus
00:10:15 7.1.2 Second fundamental theorem of calculus
00:10:43 7.2 Calculating integrals
00:11:39 8 Extensions
00:12:07 8.1 Improper integrals
00:12:21 8.2 Multiple integration
00:13:03 8.3 Line integrals
00:14:27 8.4 Surface integrals
00:15:09 8.5 Contour integrals
00:15:37 8.6 Integrals of differential forms
00:16:33 8.7 Summations
00:17:01 9 Computation
00:17:15 9.1 Analytical
00:17:43 9.2 Symbolic
00:18:11 9.3 Numerical
00:18:53 9.4 Mechanical
00:19:21 9.5 Geometrical
00:19:35 10 See also
00:20:03 11 References
00:20:45 12 Bibliography
00:21:13 13 External links
00:21:41 13.1 Online books
00:22:09 Integrals of differential forms
00:22:51 Summations
00:23:19 Computation
00:23:33 Analytical
00:24:01 Symbolic
00:24:29 Numerical
00:25:11 0...2
00:25:39 0. However, the substitution u
00:26:07 Mechanical
00:26:35 Geometrical
00:27:03 See also



Listening is a more natural way of learning, when compared to reading. Written language only began at around 3200 BC, but spoken language has existed long ago.

Learning by listening is a great way to:
- increases imagination and understanding
- improves your listening skills
- improves your own spoken accent
- learn while on the move
- reduce eye strain

Now learn the vast amount of general knowledge available on Wikipedia through audio (audio article). You could even learn subconsciously by playing the audio while you are sleeping! If you are planning to listen a lot, you could try using a bone conduction headphone, or a standard speaker instead of an earphone.

Listen on Google Assistant through Extra Audio:
https://assistant.google.com/services/invoke/uid/0000001a130b3f91
Other Wikipedia audio articles at:
https://www.youtube.com/results?search_query=wikipedia+tts
Upload your own Wikipedia articles through:
https://github.com/nodef/wikipedia-tts
Speaking Rate: 0.9985191521869616
Voice name: en-AU-Wavenet-C


"I cannot teach anybody anything, I can only make them think."
- Socrates


SUMMARY
=======
In mathematics, an integral assigns numbers to functions in a way that can describe displacement, area, volume, and other concepts that arise by combining infinitesimal data. Integration is one of the two main operations of calculus, with its inverse operation, differentiation, being the other. Given a function f of a real variable x and an interval [a, b] of the real line, the definite integral





∫

a


b


f
(
x
)

d
x


{\displaystyle \int _{a}^{b}f(x)\,dx}
is defined informally as the signed area of the region in the xy-plane that is bounded by the graph of f, the x-axis and the vertical lines x = a and x = b. The area above the x-axis adds to the total and that below the x-axis subtracts from the total.
The operation of integration, up to an additive constant, is the inverse of the operation of differentiation. For this reason, the term integral may also refer to the related notion of the antiderivative, a function F whose derivative is the given function f. In this case, it is called an indefinite integral and is written:




F
(
x
)
=
∫
f
(
x
)

d
x
.


{\displaystyle F(x)=\int f(x)\,dx.}
The integrals discussed in this article are those termed definite integrals. It is the fundamental theorem of calculus that connects differentiation with the definite integral: if f is a continuous real-valued function defined on a closed interval [a, b], then, once an antiderivative F of f is known, the definite integral of f over that interval is given by





∫

a


b



f
(
x
)
d
x
=


[

F
(
x
)

]


a


b

...